Квадрат суммы

Квадрат суммы двух выражений равен квадрату первого, плюс удвоенное произведение первого и второго, плюс квадрат второго: (a + b)² = a² + 2ab + b²

Для доказательства справедливости формулы квадрата суммы достаточно перемножить выражения раскрыв скобки:

(a + b)² = (a + b)·(a + b) = a² + ab + ba + b² = a² + 2ab + b²

Формулу квадрата суммы удобно использовать:

• для раскрытия скобок
• для упрощения выражений
• для вычисления квадратов больших чисел, не используя калькулятор или умножение в столбик

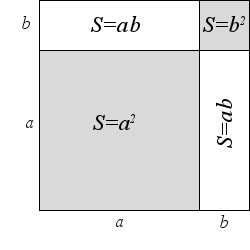Формулу квадрата суммы двух положительных чисел a и b можно изобразить геометрически

Рассмотрим квадрат со стороной (a + b), его площадь равна (a + b)².

В противоположных углах рассматриваемого квадрата построим квадраты со сторонами a и b.

Тогда большой начальный квадрат, будет разделен на четыре части: два квадрата с площадями a² и b², а также два прямоугольника с площадями равными ab. Тогда получаем, что

(a + b)² = (a + b)·(a + b) = a² + b² + ab+ ab = a² + 2ab + b²

Раскрыть скобки (x + 3)².

Решение:

(x + 3)² = x² + 2·3·x + 3² = x² + 6x + 9

Раскрыть скобки (2x + 3y²)².

Решение:

(2x + 3y²)² = (2x)² + 2·(2x)·(3y²) + (3y²)² = 4x² + 12xy² + 9y⁴

Упростить выражение 9x² + 6x + 1(3x + 1).

Решение:

Можно заметить, что выражение в числителе - это разложенный квадрат суммы

9x² + 6x + 1(3x + 1) = (3x + 1)²(3x + 1) = 3x + 1

Вычислить 71².

Решение:

71² = (70 + 1)² = 70² + 2·70·1 + 1² = 4900 + 140 + 1 = 5041