Смешанное произведение векторов.

Определение. Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.

Формулы вычисления смешанного произведения векторов

Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.

Смешанное произведение векторов a = {a_x; a_y; a_z}, b = {b_x; b_y; b_z} и c = {c_x; c_y; c_z} в декартовой системе координат можно вычислить, используя следующую формулу:

a · [b × c] =	a_x	a_y	a_z
	b_x	b_y	b_z
	c_x	c_y	c_z

Свойства смешанного произведения векторов

Геометрический смысл смешанного произведения.
Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами:
V_парал = |a · [b × c]|
Геометрический смысл смешанного произведения.
Объем пирамиды образованной тремя векторами a, b и с равен одной шестой части от модуля смешанного произведения этих векторов:

V_пир = 1 |a · [b × c]|
6
Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.
a · [b × c] = b · (a · c) - c · (a · b)
a · [b × c] = b · [c × a] = c · [a × b] = -a · [c × b] = -b · [a × c] = -c · [b × a]
a · [b × c] + b · [c × a] + c · [a × b] = 0 - тождество Якоби.

Примеры задач на вычисления смешанного произведения векторов

Пример 1. Найти смешанное произведение векторов a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.

Решение:

a · [b × с] =	1	2	3	=
	1	1	1
	1	2	1

= 1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2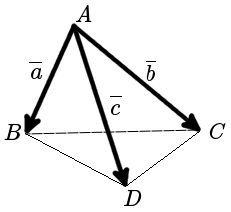

Пример 2.

Найти объем пирамиды построенной на векторах a = {1; 2; 3}, b = {1; -1; 1}, c = {2; 0; -1}.

Решение: Найдем смешанное произведение этих векторов:

a · [b × с] =	1	2	3	=
	1	-1	1
	2	0	-1

= 1·(-1)·(-1) + 2·1·2 + 3·1·0 - 3·(-1)·2 - 2·1·(-1) - 1·1·0 =

= 1 + 4 + 0 + 6 + 2 - 0 = 13

Найдем объем пирамиды воспользовавшись свойствами:

V_пир =	1	\|a · [b × c]\| =	13	= 2	1
	6		6		6

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!