Изучение математики онлайн.
Изучайте математику с нами и убедитесь: "Математика - это просто!"
 |
Расстояние от точки до плоскости.Навигация по странице:
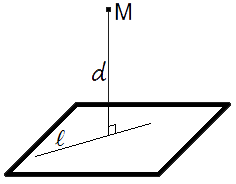 Определение. Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.Формула для вычисления расстояния от точки до плоскостиЕсли задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(Mx, My, Mz) до плоскости можно найти, используя следующую формулу:
Примеры задач на вычисление расстояния от точки до плоскостиПример 1. Найти расстояние между плоскостью 2x + 4y - 4z - 6 = 0 и точкой M(0, 3, 6).
Решение. Подставим в формулу коэффициенты плоскости и координаты точки
Ответ: расстояние от точки до плоскости равно 3. Аналитическая геометрия: Вступление и оглавлениеРасстояние между двумя точками.Середина отрезка. Координаты середины отрезка.Уравнение прямой.Уравнение плоскости.Расстояние от точки до плоскости.Расстояние между плоскостями.Расстояние от точки до прямой на плоскости.Расстояние от точки до прямой в пространстве.Угол между плоскостями.Угол между прямой и плоскостью.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! |
 |
|||||||||||||||||||||||||||||||||||||||||||||