Квадратное уравнение

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a≠0.

• Геометрический смысл

• Вывод формулы для решения квадратного уравнения

• Нахождение корней квадратного уравнения

• Теорема Виета

• Разложение квадратного уравнения на множители

Геометрический смысл

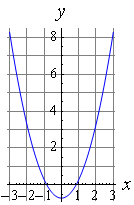Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют точки пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня.

Если коэффициент а положительный, ветви параболы направлены вверх, если отрицательный — ветви параболы направлены вниз. Если коэффициент b положительный, то вершина параболы лежит в левой полуплоскости, если отрицательный — в правой полуплоскости.

Вывод формулы для решения квадратного уравнения

Формулу для решения квадратного уравнения можно получить так

      ax² + bx + c = 0
      ax² + bx = -c

Умножим уравнение на 4a

      4a²x² + 4abx = -4ac
      4a²x² + 4abx + b² = -4ac + b²
      (2ax + b)² = b² -4ac
      2ax + b = ±$\sqrt{b^2-4 a c}$

Нахождение корней квадратного уравнения

Квадратное уравнение с вещественными коэффициентами может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта D = b² − 4ac:

• при D > 0 корней два, и они вычисляются по формуле

  x1,2 =  -b ± √D 2a

• при D = 0 корень один (два равных или совпадающих корня), кратности 2:

  x =  -b 2a

• при D < 0 вещественных корней нет. Существуют два комплексных корня, выражающиеся формулой

  x1,2 =  -b ± i√-D 2a

Например. Найти корни квадратного уравнения: 2x² + 5x + 3 = 0
D = 5² - 4·3·2 = 25 - 24 = 1

x1 =  -5 + √1  = -1, 2·2

x2 =  -5 - √1  = -1 1 2·2 2

Упражнения. Квадратные уравнения.

Теорема Виета

Сумма корней приведённого квадратного уравнения x² + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
      x₁ + x₂ = -p,      x₁x₂ = q.

Разложение квадратного уравнения на множители

Если известны оба корня квадратного уравнения, его можно разложить по формуле
      ax² + bx + c = a(x - x₁)(x - x₂)